Popular matchings with weighted voters
Klaus Heeger, Ágnes Cseh
Abstract
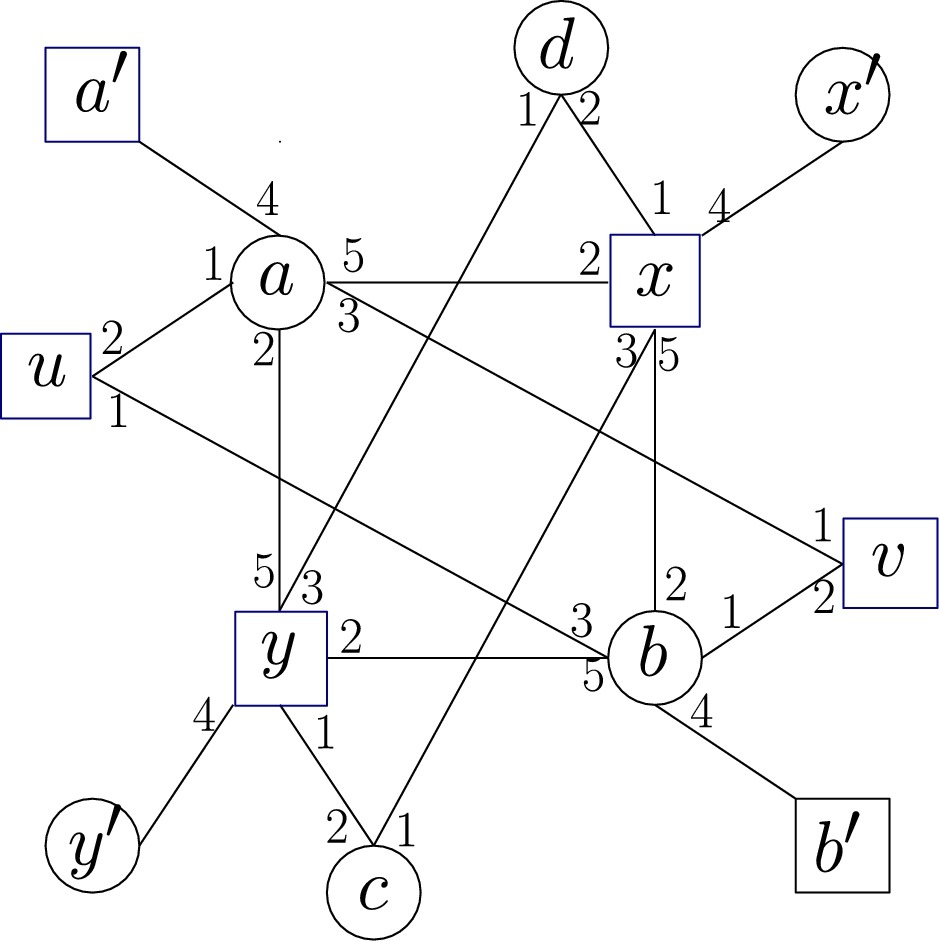
We consider a natural generalization of the well-known POPULAR MATCHING problem where every vertex has a weight. We call a matching more popular than matching ′ if the weight of vertices preferring to ′ is larger than the weight of vertices preferring ′ to . For this case, we show that it is NP-hard to find a popular matching. Our main result is a polynomial-time algorithm that delivers a popular matching or a proof for its non-existence in instances where all vertices on one side have weight for some > 3 and all vertices on the other side have weight 1.
Keywords: Popular matching, Stable matching, Complexity, Algorithm