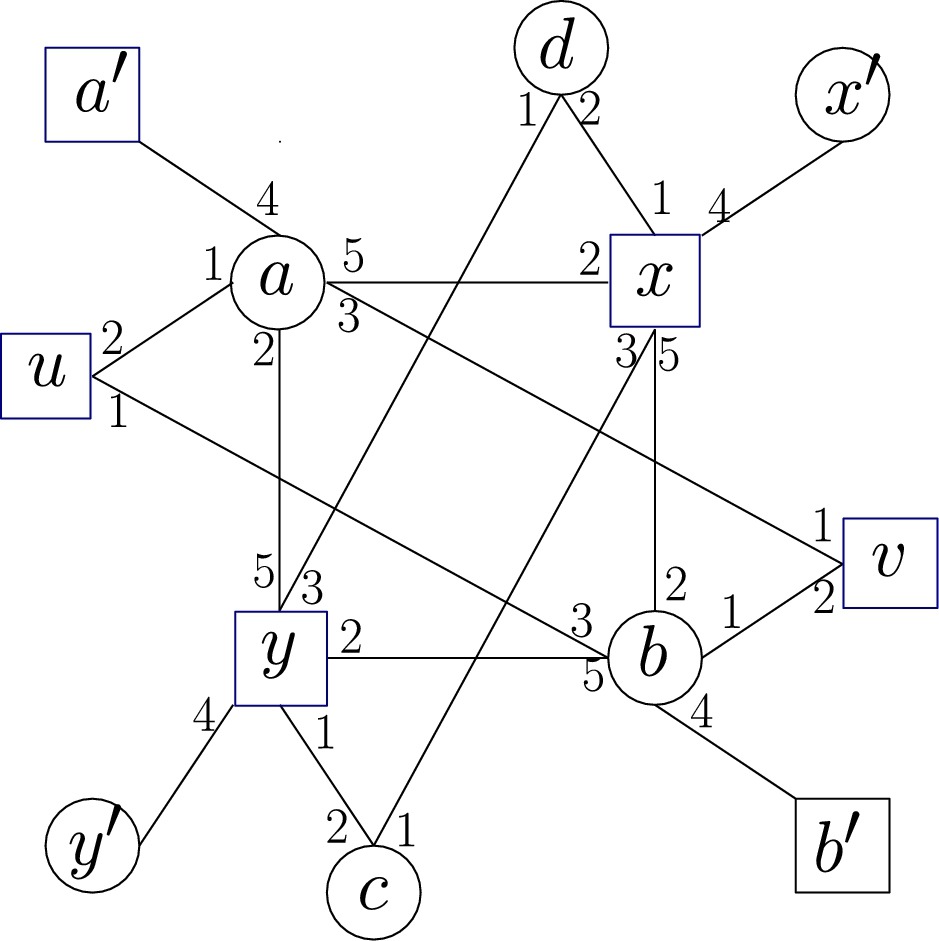
Our input is a complete graph G on n vertices where each vertex has a strict ranking of all other vertices in G. The goal is to construct a matching in G that is “globally stable” or popular. A matching M is popular if M does not lose a head-to-head election against any matching M’: here each vertex casts a vote for the matching in {M,M’} in which it gets a better assignment. Popular matchings need not exist in the given instance G and the popular matching problem is to decide whether one exists or not. The popular matching problem in G is easy to solve for odd n. Surprisingly, the problem becomes NP-hard for even n, as we show here. This seems to be the first graph theoretic problem that is efficiently solvable when n has one parity and NP-hard when n has the other parity.
