New article by Péter Biró, and Gergely Csáji in the journal Games and Economic Behavior

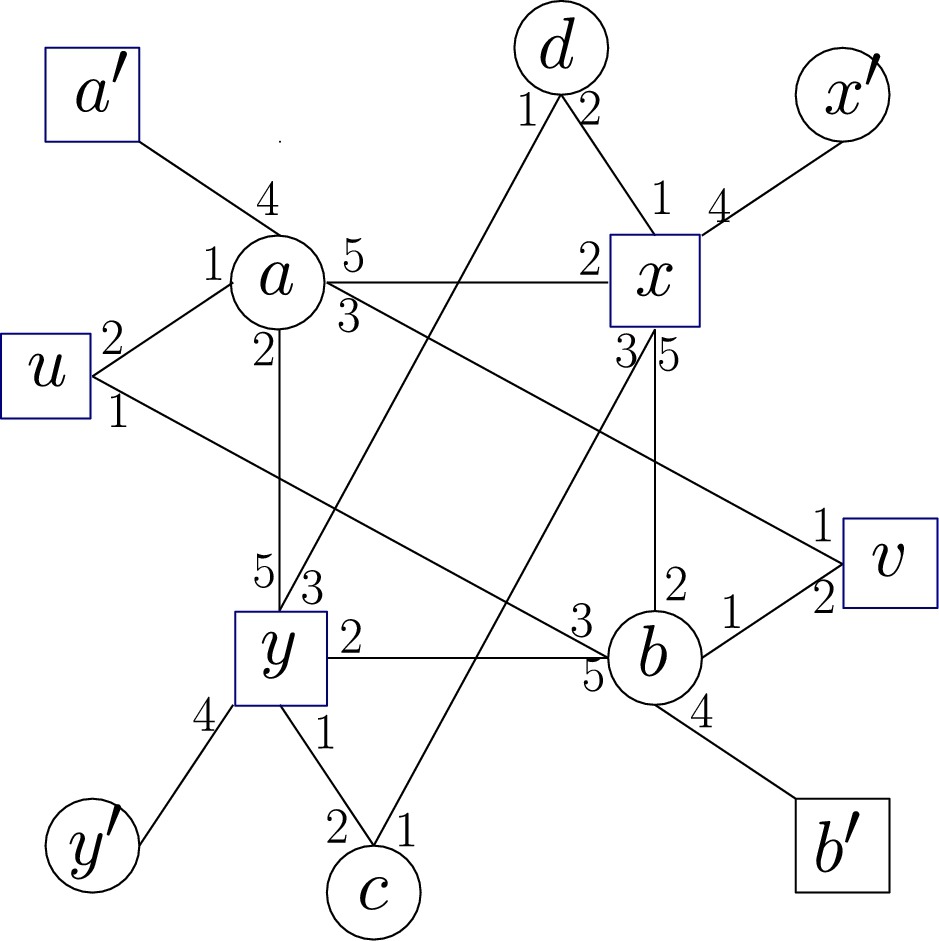
We study strong core and Pareto-optimal solutions for multiple partners matching problem under lexicographic preference domains from a computational point of view. The restriction to the two-sided case is called stable many-to-many matching problem and the general one-sided case is called stable fixtures problem. We provide an example to show that the strong core can be empty even for many-to-many problems, and that deciding the non-emptiness of the strong core is NP-hard. On the positive side, we give efficient algorithms for finding a near feasible strong core solution and for finding a fractional matching in the strong core of fractional matchings. In contrast with the NP-hardness result for the stable fixtures problem, we show that finding a maximum size matching that is Pareto-optimal can be done efficiently for many-to-many problems. Finally, we show that for reverse-lexicographic preferences the strong core is always non-empty in the many-to-many case.